 科学
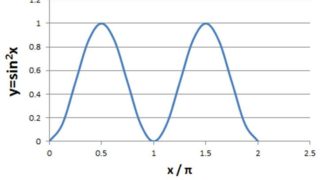
科学 y=sin2xのグラフや周期は?y=sin2θを微分するとどうなるのか?
数学の問題を解いたり、科学的な解析を行ったりする際に、よく三角関数の計算が必要となることが多いです。 中でも、三角関数を含んだ数式のグラフや微分の方法についての問題が出ることが多く、その解法について理解しておくといいです。 ここでは、この三...
 科学
科学  科学
科学  科学
科学  科学
科学  科学
科学  科学
科学  科学
科学  科学
科学  科学
科学  科学
科学