sinθ+√3cosθの最大値や最小値の計算方法は？sinθ+√3cosθ＝0を解けと言われた場合の対処方法は？【sinθ+√3cosθの合成とが1となるθは？】

数学の問題を解いたり、科学的な解析を行ったりする際に、よく三角関数の計算が必要となることが多いです。

中でも、三角関数を含んだ数式のグラフや微分の方法についての問題が出ることが多く、その解法について理解しておくといいです。

ここでは、この「三角関数を含んだ式の一つであるsinθ+√3cosθの合成方法」やこの「sinθ+√3cosθの最大値や最小値の計算方法」「sinθ+√3cosθ＝0や1となる時の対処方法」について確認していきます。

sinθ+√3cosθを合成するとどうなるか

sinθ+√3cosθの最大値や最小値の計算を行っていく前に、まずはsinθ+√3cosθを合成して一つの変数の式にするといいです。

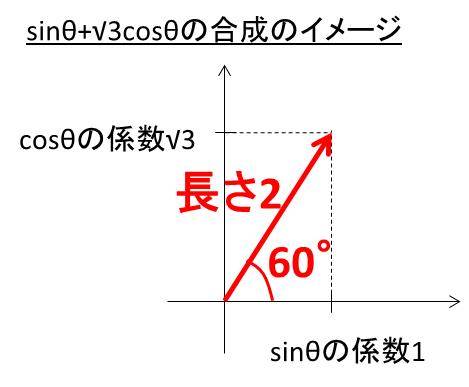
具体的に三角関数の合成はこちらにも記載していますが、sinの係数をx軸にとり、cosの係数をy軸にとり（つまり1,、ルート3）、ベクトルを作った場合の長さとx軸となる角に着目していきます。

今回では、長さが2、角度が30度（π/6）となるために、sinθ+√3cosθ＝2sin（θ+π/3（60°））と合成することができました。

上で、sinθ+√3cosθの合成方法について解説しましたので、これを用いてsinθ+√3cosθ＝1やsinθ+√3cosθ＝0を解いていきます。

2sin（θ+π/3）＝1を解けばいいこととなり、（θ+π/3）＝1/2と式変形できることから（θ+π/3＝1/6π、5/6π）と求められます。θの範囲と指定すると、0＜θ＜πの場合はθ＝5/6πが解となるのです。

同様の考え方から、sinθ+√3cosθ＝0となるケースでは、sin（θ+π/3）＝0を考慮すればよく、θ+π/3＝0、πより、θ＝2/3πと求めることができました。

このように、sinθ+√3cosθは合成した後の2sin（θ+π/3）を考えるといいです。

ここで0≦θ≦πという条件であるとすると、2sin（θ+π/3）のsin（θ+π/3）の部分の数値は以下の図の範囲を取ることがわかります。

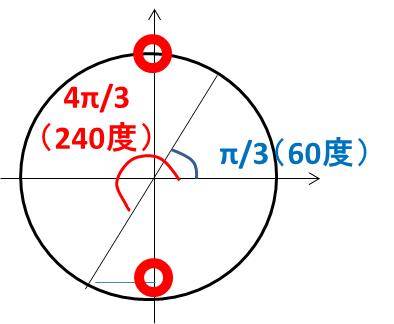
最大値はθ+π/3＝π/2のとき、最小値はθ+π/3＝π+π/3のときとなるのがわかるでしょう。

よって、最大値はθ＝π/6の際に2、最小値はθ＝πの時に－√3/2と求めることができるのです。

ここでは、「三角関数を含んだ式の一つであるsinθ+√3cosθの合成方法」やこの「sinθ+√3cosθの最大値や最小値の計算方法」「sinθ+√3cosθ＝0や1となる時の対処方法」について解説しました。

・sinθ+√3cosθ＝2sin（θ+π/3）と合成できる
・最小値、最大値はこれを元に計算すればいい
・sinθ+√3cosθ＝0や1となる時の解き方も上と同じ

です。

三角関数の扱いに慣れ、数学をより好きになっていきましょう。