数学、算数、SPIなどの試験において、様々な計算が求められることがあります。
例えば、ある池の周りをある二人が反対方向に向かい出会う計算や、逆に同じ方向に向かい追いつく際の速さを求める問題がよく出題されます。
このような状況下ではどう求めていけばいいのか理解していますか。
ここでは、池の周りの速度や時間に関する計算問題の解き方について確認していきます。
池の周りを反対方向に進み、出会う時間の計算方法【速度】
それでは早速、練習問題を解くことによって、同じ地点から反対方向に歩く二人が出会うまでの時間を考えていきます。
・例題1
あの池の周りは3600mあります。
同じ地点にaさんとbさんが立ち、同時に反対方向に向かって歩き始めました。
aさんの速度が1m/sでbさんの移動する速さが2m/sの場合、何分後に出会うのか計算していきましょう。
・解答1
まずは、二人が近づいている速さを求めていきます。なお、状況がわからないケースでは、以下のよう図を描いてイメージしやすくするのもおすすめです。
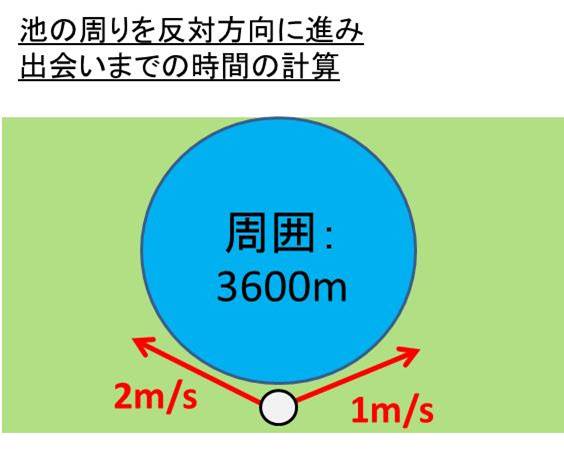
反対の方向に向かっているため、各々の速度を足しあらせることで速度が計算できます。
具体的には、1+2=3m/s が近づく際の速度となるのです。
よって、池の周りを違う方向に歩いて出会うまでの時間は 3600 / 3 = 1200s = 20分と計算することができました。
池の周りを同じ方向に進み、一方が追いつくまでの時間の計算方法【速度】
今度は、池の周りを同じ同じ地点から同じ方向に歩く二人において、一方がもう一方に追いつき、追い越すまでの時間を求めていきましょう。
・例題1
あの池の周りは1000mあります。
同じ地点にaさんとbさんが立ち、同時に同じ方向に向かって歩き始めました。
aさんの速度が4m/sでbさんの移動する速さが2m/sの場合、何分後に出会うのか計算していきましょう。
・解答1
まずは、二人の速度の差を求めていきます。
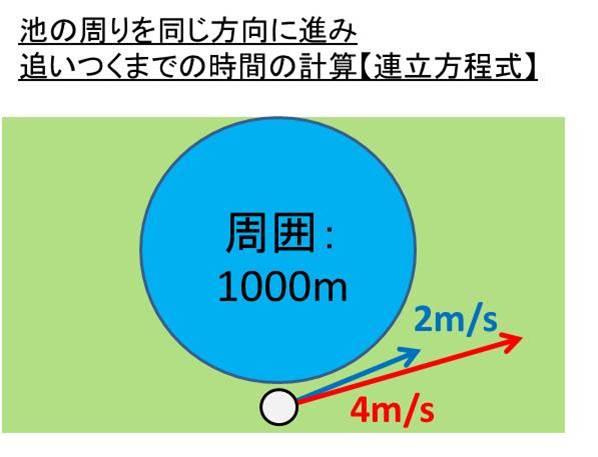
同じの方向に向かっているため、各々の速度を引くことで速度が計算できます。
具体的には、4-2=2m/s が追いついている速度となるのです。
よって、池の周りを違う方向に歩いて出会うまでの時間は 1000 / 2= 500s = 8分20秒と計算することができました。
なお、これらの池の周りの速さ、時間の計算問題は旅人算と呼ばれるものに分類されることも理解しておくといいです。
基本的には、何が起きているのかを丁寧に数値化していけば、計算できます。
まとめ 池の周りにて出会う・追い越すの計算問題【連立方程式】
ここでは、池の周りを同じ方向、反対方向に向かう時の時間に関する問題の解き方について確認しました。
いずれも、図を描いたりして、その時にどのような状況になっているのかをきちんと把握することが大切です。
池の周りでの連立方程式を用いた計算を行うことによって、日々の生活に役立てていきましょう。

コメント