算数や数学などにおいてよく立方体に関係する問題が出題されることがあります。
例えば、立方体の表面積や体積を計算する場面が中でも多いですが、これらを計算するための公式た具体的な計算方法について理解していますか。
ここでは、立方体の表面積や体積を求める方法やその単位とお関係性について計算問題付で解説していきます。
立方体の表面積を求める公式と計算方法
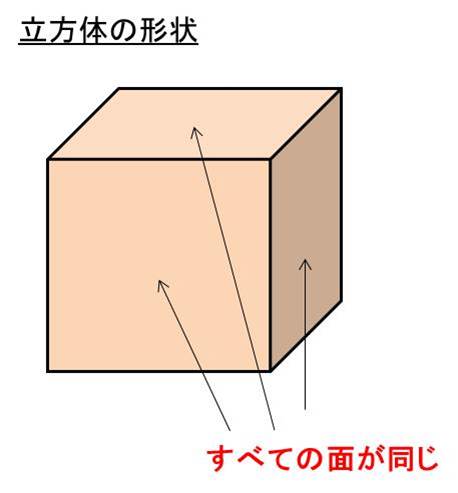
立方体とはご存知の通り以下のようなすべての面が同じ形状の立体です。
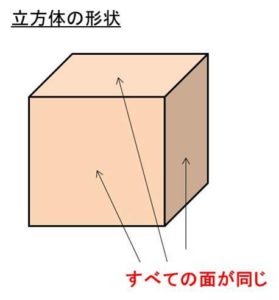
そして、立方体の面の数は合計6つあることがわかるでしょう(見えている部分も3つと裏からみた場合の3つ)。
かつ、立方体の一つの面は正方形であることから、立方体の一つの面の面積=1辺×1辺の長さで計算できます。
そのため、立方体の表面積=1辺×1辺×6という公式で計算可能です。
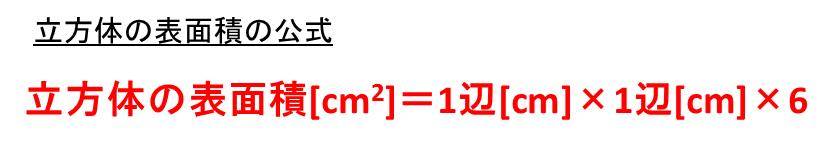
立方体の表面積の単位のワンポイントアドバイス
なお、立方体の表面積の単位として、上ではcm2(平方センチメートル)で表していますが、1辺の長さがm(メートル)である場合はその表面積の単位もm2(平方メートル)と換算できることも覚えておきましょう。
ちなみに、1m2=10000cm2という関係性があります。
立方体の表面積の計算問題を解いてみよう
それでは、立方体の表面積の求め方に慣れるためにも計算問題を解いていきましょう。
・例題1
1辺の長さが4cmの立方体の表面積はいくらでしょうか。
・解答1
上の立方体の表面積の公式を元に計算していきます。
4×4×6=96cm2(平方センチメートル)
と求めることができるのです。
1辺の長さの単位がm(メートル)の場合の立方体の表面積も計算していきましょう。
・例題2
1辺の長さが5mの立方体の表面積をいくらと計算できるでしょうか。
・解答2
5 × 5 × 6= 150m2(平方メートル)と換算できました。
わからない場合では、以下のように図にして見るのもおすすめです。
立方体の体積を求める公式と計算方法
続いては、立方体の体積の求め方について考えていきましょう。
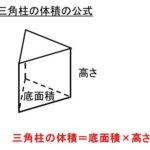
立方体を始めとした立体の体積は底辺の縦の長さ×底辺の横の長さ×高さ(縦×横×高さ)で計算できます。
ただ、立方体ではすべての辺の長さが同じであるために立方体の体積=1辺の長さ×1辺の長さ×1辺の長さという公式で求められるのです。

立方体の体積の単位のワンポイントアドバイス
なお、立方体の体積の単位として、上ではcm3(立方センチメートル)で表していますが、1辺の長さがm(メートル)である場合はその表面積の単位もm3(立方メートル)と換算できることも覚えておきましょう。
ちなみに、1m3=1000000cm3という関係性があります。
立方体の体積の計算問題を解いてみよう
それでは、立方体の体積の求め方に慣れるためにも計算問題を解いていきましょう。
・例題3
1辺の長さが2cmの立方体の体積はいくらでしょうか。
・解答3
上の立方体の体積の公式を元に計算していきます。
2×2×2=8cm3(立方センチメートル)
と求めることができるのです。
1辺の長さの単位がm(メートル)の場合の立方体の表面積も計算していきましょう。
・例題4
1辺の長さが3mの立方体の体積はいくらと計算できるでしょうか。
・解答4
3 × 3 × 3= 27m3(立方メートル)と換算できました。
わからない場合では、以下のように図にして見るのもおすすめです。
まとめ 立方体の表面積と体積の公式と単位と計算方法
ここでは、立方体の表面積と体積と公式と単位と計算方法について確認しました。
・立方体の表面積=1辺の長さ×1辺の長さ×6
・立方体の体積=1辺の長さ×1辺の長さ×1辺の長さ
と単位変換(換算)できます。
単位換算に慣れ、業務の効率化を図っていきましょう。

コメント