確率・場合の数の計算を行う際に、C(組み合わせの数の計算)などの記載を見かけることがあるでしょう。
この記号Cを含む計算方法は意外と難しいと感じる人が多いですが、あなたは理解できていますか。
ここでは、このCを含んだ組み合わせの順列の計算方法として6C1・6C2・6C3・6C4・6C5・6C6・6C0の計算方法・答え・読み方・意味について解説していきますので、参考にしてみてください。
6C2の計算方法・答え・読み方・意味は?【組み合わせ】
それでは以下で6C2の計算方法・答え・読み方・意味などの各種情報について確認していきます。
6C2とは6×5/ (2×1) と
・分子に6を始めとして5と、1ずつ減らしたもの「2つ」を掛け算する計算
・分母に2を始めとした階乗の計算(1になるまで1ずつ減らしつ掛け算)
・分子/分母
を行った値であり、その答えは15です。

6C2の読み方はそのまま「ろくしーに」と表現すればいいです。
計算間違いに注意しましょう。
6C4の計算方法・答え・読み方・意味は?6C2との関係は?【組み合わせ】
続いて、今度はCを含んだ組み合わせの計算方法として、6C4の計算方法・答え・読み方・意味などの各種情報について確認していきます。
結論からいいますと、6C4の答えは6C2と同じであり、15となります(nCr=nCn-rの規則より)。
6C4の読み方はそのまま「ろくしーよん」と表現すればいいです。

6C3の計算方法・答え・読み方・意味は?6C2との関係は?【組み合わせ】
続いて、今度はCを含んだ順列の計算方法として、6C3の計算方法・答え・読み方・意味などの各種情報について確認していきます。
6C3の計算方法も同様で5×4×3 / (3×2×1)=20が答えとなります。

6C3の読み方はそのまま「ろくしーさん」と表現すればいいです。
6C1の計算方法・答え・読み方・意味は?【順列】
続いて、今度はCを含んだ組み合わせの計算方法として、6C1の計算方法・答え・読み方などの各種情報について確認していきます。
結論からいいますと、6C1の答えは6となります。

例えば、5つのカード(a,b,c,d,e,f)の中から1つ選ぶ組み合わせは、a,b,c,d,e,fの5通りとなるため、これが答えとなるわけですね。
6C1の読み方はそのまま「ろくしーいち」と読むといいです。
なお、上の組み合わせの記号のCでは6Cr=6C(5-r)という規則が成り立つことから、6C1と後に解説の6C5は同じ計算となります。
6C5の計算方法・答え・読み方・意味は?6C1との関係性は?【順列】
続いて、今度はCを含んだ順列の計算方法として、6C5の計算方法・答え・読み方・意味などの各種情報について確認していきます。
結論からいいますと、6C5=6C1=6となります。

6C5の読み方はそのまま「ろくしーご」と表現すればいいです。
6C0の計算方法・答え・読み方・意味は?【順列】
続いて、今度はCを含んだ順列の計算方法として、6C0の計算方法・答え・読み方・意味などの各種情報について確認していきます。
答えからいいますと、6C0=1となります。

6C0とは「6つのカードの中から0個を選ぶ組み合わせの数」、つまり「1つも選ばない数」を意味しているため、1通りのみが答えとなるわけです。
6C0だけでなく、nC0では必ず1となると覚えておきましょう。
6C0の読み方はそのまま「ろくしーぜろ」と表現すればいいです。
6C6の計算方法・答え・読み方・意味は?【順列】
続いて、今度はCを含んだ順列の計算方法として、6C6の計算方法・答え・読み方・意味などの各種情報について確認していきます。
結論からいいますと、6C6=6C0=1となります。

6C6とは、上の6C0などの考え方として同様ですが、「6つのカードの中から6個を選ぶ組み合わせの数」、つまり「すべてを選ぶ組み合わせの数」を意味しているため、1通りのみが答えとなるわけです。
6C6だけでなく、nCnでは必ず1となると覚えておきましょう。
6C6の読み方はそのまま「ろくしーろく」と表現すればいいです。
まとめ 6C3や6C4や6C5や6C6や6C1の計算方法・答え・読み方も解説!【確率・場合の数・組み合併せ】
ここでは、6C1・6C2・6C3・6C4・6C5・6C6・6C0の計算方法・答え・読み方について解説しました。
どれも良く出てくる計算のため、この機会に理解しておくといいです。
組み合わせを始めとしたさまざまな計算方法になれ、日々の生活に役立てていきましょう。

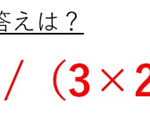
コメント