数学の問題を解いたり、科学的な解析を行ったりする際に、よく三角関数の計算が必要となることが多いです。
中でも、三角関数を含んだ数式のグラフや微分の方法についての問題が出ることが多く、その解法について理解しておくといいです。
ここでは、この三角関数を含んだ式の一つであるy=1/cosθ(1/cos x)やy=1/sinθ(1/sin x)の微分の公式や計算方法にについて確認していきます。
1/cosθ(1/cosx)を微分するとどうなるのか【計算方法や公式】
それでは、まず1/cosθというcosθの逆数の式の微分について考えていきます。
なお1/cosθではなく1/cosxという表記の場合もありますが、単純に変数の表記が違うだけで意味は同じことを理解しておくといいです。他の表記としては1/cosθはsecθと、1/sinθはcosec θとも表現することも覚えておきましょう。
1/cosθ=cosθ^-1とも記載することができることから、この微分は(cosθ^-1)’=-cosθ^-2(cosθ)’=sinθ/cosθ^2となるのです。

cosθの肩の係数がマイナス1の数値が1/cosθであること、肩の係数を減らした後にcosθを微分したものを掛け合わせることも忘れないようにしましょう。
1/sinθ(1/sinx)を微分するとどうなるのか【計算方法や公式】
それでは、まず1/sinθというsinθの逆数の式の微分について考えていきます。
上述の1/cosθのように1/sinθではなく1/sinxという表記の場合もありますが、こちらもに変数の表記が違うだけと覚えておくといいです。
ここで1/sinθ=sinθ^-1とも記載することができることから、この微分は(sinθ^-1)’=-sinθ^-2(sinθ)’=-cosθ/sinθ^2となるのです。
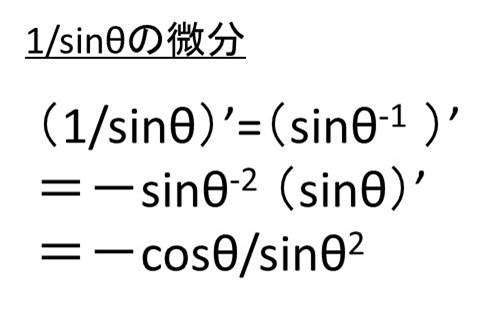
上の1/cosの微分と同じようsinθの肩の係数がマイナス1の数値が1/sinθであること、肩の係数を減らした後にsinθを微分したものも掛け合わせることも忘れないようにしましょう。
両方ともの計算方法をまとめて理解しておくと効率的です。
まとめ 1/cosθ(sec θ)の微分は?1/sinθ(cosec θ)の微分は?【1/cosxや1/sinx】
ここでは1/cosθ(1/cosx)の微分の方法、1/sinθ(1/sinx)の微分の方法について確認しました。
・1/cosθは1/cosxと書いたり、secθとも表す
・1/sinθは1/sinxと書いたり、cosecθとも表す
・1/cosθの微分はsinθ/cosθ^2
・1/sinθの微分は-cosθ/sinθ^2
となることを理解しておきましょう。
結果は忘れても導出方法を理解しておけば問題ないです。
各種三角関数を含んだ計算に慣れ、数学をより楽しんでいきましょう。
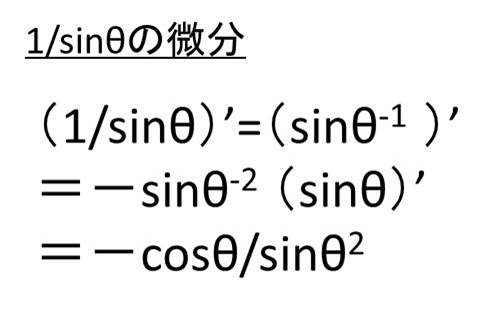
コメント