y=sinθ+cosθの最大値や最小値を求める方法は？sinθ+cosθ=1のθを計算する方法【sinθとcosθの合成やその範囲】

数学の問題を解いたり、科学的な解析を行ったりする際に、よく三角関数の計算が必要となることが多いです。

中でも、三角関数を含んだ三角方程式の問題が出ることが多く、その解法について理解しておくといいです。

ここでは「三角方程式の一つであるy=sinθ+cosθの最大値や最小値を求める問題」や「sinθ+cosθ=1の方程式の解き方」について、関連する方法のsinθとcosθの合成のやり方も併せて解説していきます。

y=sinθ+cosθの最大値を計算してみよう（0≦θ≦π/4）【sinθとcosθの合成やその範囲】

まず、y=sinθ+ cosθ（0≦θ≦1）の最大値を計算するには、三角関数の合成の考え方を活用するといいです。

具体的には、以下のような図を下記、sinθの係数をyに、cosθの係数をxにした際のベクトルの長さとその角度を見ることで、sinとして合成したものに変換することができます。

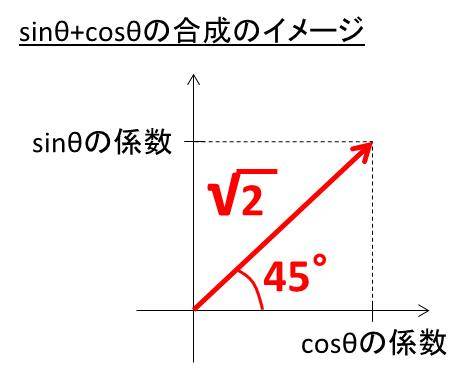
今回は長さ√2、角度45度となるため、y=sinθ+ cosθ＝√2 sin（θ+45）と計算することができるのです。

θ+45＝tとおくと、三角関数を合成した後の範囲は、π/4 ≦t≦π/2と変換されます。

すると、y=sinθ+ cosθ＝√2 sint（範囲 π/4≦t≦π/2）では、ｔ＝π/4の時に最小値の√2× √2/2＝１となります。

一方で最大値はt＝π/2の時に、√2×1＝√2と計算することができました。

これが三角方程式y=sinθ+cosθなどの数値がとる範囲の考え方といえます。

sinθ+cosθ=1を解いていくためには、上と同様に三角関数の合成の考え方を採用していきます。

結局のところsinθ+cosθ＝√2 sin（θ+45）と求めることができるため、これが1となるようなθを計算すればいいわけです。

√2 sin（θ+45）＝1より、sin（θ+45）＝√2/2 となればよく、θ+45＝30度もしくは150度と求めることができるわけです。

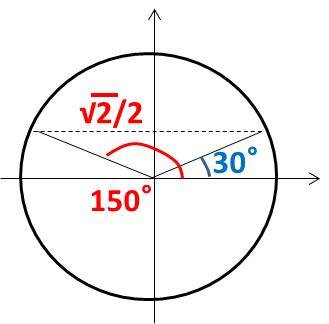
今回のθの範囲が、0≦θ≦πとなることを考慮すると、θ＝105度が解とわかるのです。

三角方程式では、合成の考え方を使う場面が多いので丁寧に理解しておくといいです。

ここでは、y=sinθ+cosθの最大値を求める方法は？sinθ+cosθ=1のθを計算する方法【sinθとcosθの合成やその範囲】について解説しました。

・これらの問題を解くには三角関数の合成を活用するといい

・sinθ+cosθ＝√2sinθ（θ+45）

・範囲が変わることも気を付ける

といいです。

y=sinθ+cosθなどの三角関数の扱いに慣れ、各種計算方法をマスターしていきましょう。