数学の問題を解いたり、科学的な解析を行ったりする際に、よく三角関数の計算が必要となることが多いです。
中でも、三角関数を含んだ数式のグラフや微分の方法についての問題が出ることが多く、その解法について理解しておくといいです。
ここでは、この三角方程式の一つであるy=cos2xのグラフやその周期、微分を行うとどうなるのかについて確認していきます。
y=cos2xのグラフや周期はどうなるのか?【y=cos2θ(2乗)のグラフ】
まず、y=cos2xは変数の部分がxの2倍になったものであり、y=cos^2xとは別の関数であることを理解しておくといいです。。またy=cos2xとy=cos2θは変数名が違うだけ意味は同じです。
代表的なx,yの数値を確認することで、y=cos2xのグラフがどうなるのかについて確認します。
まずは、
・x=0の場合はcos0度となるため、y=cos2x=1となります。
・x=15度の場合はy=cos30度となるためy=cos2x=√3/2となります。
・x=30度の場合はy=cos60度となるためy=cos2x=1/2となります。
・x=45度の場合はy=cos90度となるので、y=cos2x=0となります。
・x=60度の場合はy=cos120度となるためy=cos2x=-1/2となります。
・x=75度の場合はy=cos150度となるので、y=cos2x=-√3/2となります。
・x=90度の場合はy=cos180度となるので、y=cos2x=-1となります。
ここから先のx=90度から180まではこれらの軌跡から戻ってくるような形になるといえます。
これをプロットしていくと、y=cos2xは以下のようなグラフとなるのです。
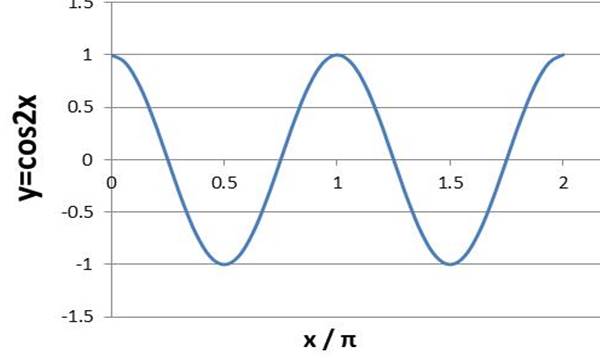
なおx=180度でy=cos2xの2xが360度と1周することになるため、周期は180度(Π)となることを理解しておくといいです。
綺麗なグラフを作成するためには、excelやpythonなどを活用していきましょう。
y=cos2x( y=cos2θ)を微分するとどうなるのか?
続いて、y= cos2xの微分についても確認していきます。
まずはcosの関数であるために、微分することによってーsinの関数への変換となります。
その上で、2xの係数をさらに微分したものを掛け合わせていけばいいことを考慮しますと、以下の通りとなるのです。
よって、y’=( cos2x)’= -sin2x(2x)’=-2sin2xと微分できました。
最後の段階で2xの微分を掛け合わせることを忘れないようにしましょう。
まとめ y=cos2xのグラフや周期は?y=cos2θを微分するとどうなるのか?
ここではy=cos2xのグラフや周期は?y=cos2θを微分するとどうなるのか?
・y=cos2xとy=cos2θは変数の表記が違うだけで同じもの
・y=cos2xを微分した形はy=-2sin2x
・y=cos2xとグラフは上の通りで周期はπ(180度)
となります。
y=cos2x(y=cos2θ)などのの方程式の扱いに慣れ、各種計算方法をマスターしていきましょう。
コメント