数学や物理などにおいて数値計算が必要となるケースは多いです。
中でも三角関数を含んだ計算を求められる割合が高いといえますが、三角関数の中身がラジアン単位の角度である場合にどう処理すればいいのか理解していますか。
ここでは、特にsin(サイン関数)の中身がラジアン単位の角度の場合の計算方法について、sin4分のπはいくらか?sin4分の3πやsin4分の5πやsin4分の7πの値は?という例題を用いて確認していきます
sin4分の1πはいくらか?【sin(1/4pi)】
それでは、sin4分のπ(ラジアン)の数値はいくらかについて確認していきます。
ラジアンの定義についてはこちらで記載していますが、πラジアン=180度といえます。
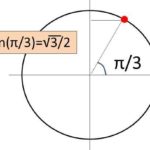
つまり、4分の1πとは度数表記では、45度を示しているわけです。なお、sin関数は円におけるyの数値を確認すればよく、角度が45度の場合では√2/2という値となります。
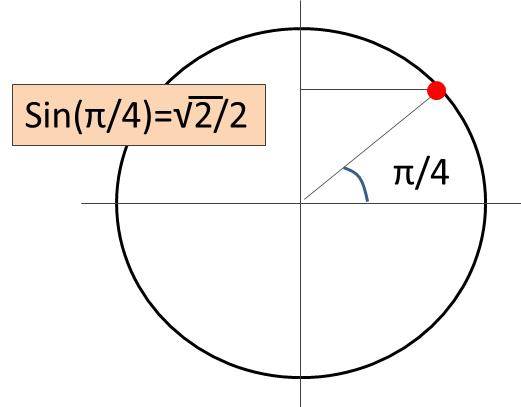
sin4分のπは三角関数の計算時によく出てくるものなので、すぐに答えられるようにしておきましょう。
sin4分の3πはいくらか?【sin(3/4pi)】
続いて、sin4分の3π(ラジアン)の数値はいくらかについて確認していきます。
上と同様に4分の3πとは度数表記では135度を示しているわけです。
なお、sin関数は円におけるyの数値を確認すればよく、角度が135度の場合では√2/2という数値となります。上のsin4分のπと同じですね。
cosと混同しないように気を付けましょう。
sin4分の5πはいくらか?【sin(5/4pi)】
続いて、sin4分の5π(ラジアン)の数値はいくらかについて確認していきます。
上と同様に4分の5πとは度数表記では225度を示していることがわかります(180度を超えているので注意するといいです)
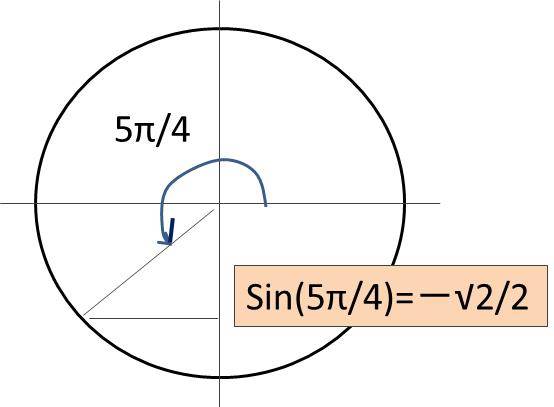
なお、sin関数は円におけるyの数値を確認すればよく、角度が225度の場合では-√2/2という数値となります。
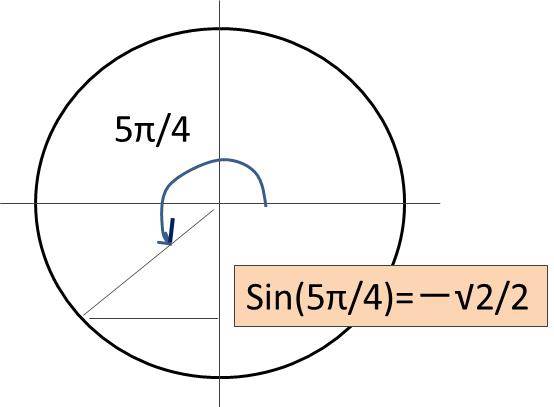
マイナスの数値をとることにも気を付けるといいです。
sin4分の7πはいくらか?【sin(7/4pi)】
最後にsin4分の7π(ラジアン)の数値はいくらかについて確認していきます。
上と同様に4分の7πとは度数表記では315度を示しているわけです。
なお、sin関数は円におけるyの数値を確認すればよく、角度が315度の場合では-√2/2という数値となります。上のsin4分の7πと同じですね。
まとめ sin4分の7πやsin4分の5πはいくらか?sin4分の3πやsin4分のπはいくらか?【sin(7/4pi) やsin(3/4pi)】
ここでは、sin4分のπはいくらか?sin4分の3πやsin4分の5πやsin4分の7πの値は?について解説しました。
・sin4分のπ:√2/2
・sin4分の3π:√2/2
・sin4分の5π:-√2/2
・sin4分の7π:-√2/2
です。
三角関数の換算式になれ、毎日の生活に役立てていきましょう。
コメント