指数関数のexpのグラフや計算方法や微分の公式まで解説【数学】

科学的な解析を行う際に、よく数値計算が必要となることがあります。

中でも指数関数のexp（自然数eの指数関数）などが苦手と感じる人が多いですが、あなたがはこの指数のexpついて理解していますか

ここでは指数関数のexpやeの意味や読み方、計算方法やグラフ、微分の公式について詳しく解説していきます。

指数関数のexpやeの意味や読み方は？

結論からいいますと、expとは自然数eを底とした指数関数の別の表記方法といえます。

一般的としては、e^x ＝ exp（x）という変換式が成り立つのです。

このexp()はexponentialの略であり、そのままエクスポーネンシャル(数値)という読み方をします。もしくは、元の形の自然数eの（数値）乗などといった具合です。

上述の通りexoの底はネイピア数e（2.718・・・）を含むため、基本的に電卓やエクセルを使用して計算する必要があります。

特にエクセルの方がより効率よく計算可能なため、覚えておくといいです。

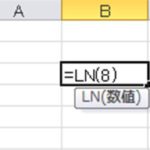
具体的にはエクセル内のセルに＝exp(数値)といれるだけで、その計算が実行されます。

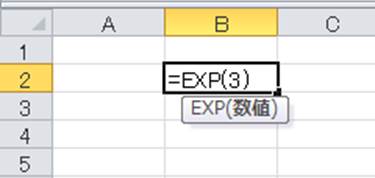
ENTERにて、以下のようにその答えが出力されます。

これが指数関数のexpの計算方法の基本形となるため、ぜひ覚えておきましょう。

なお、expを始めとした指数関数はそのグラフも併せて理解しておくといいです。

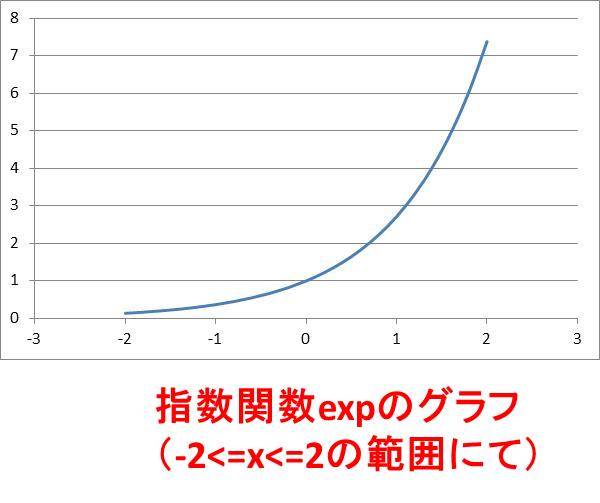
expのグラフは以下のようになります。

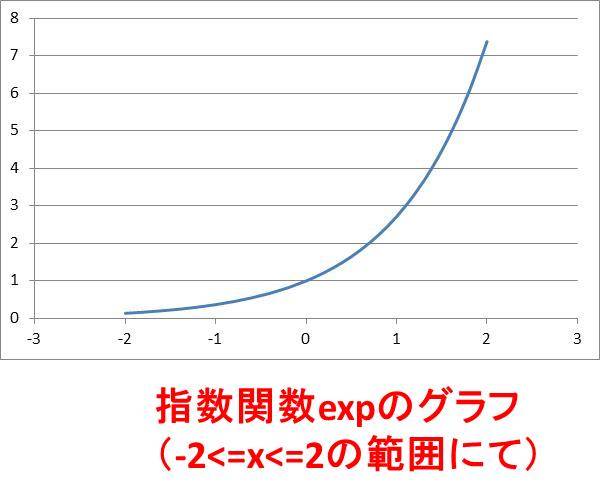
このexpのグラフをエクセルにて作るには以下の手順を踏んでいくといいです。

今回はxの数値範囲を―２～２としてそのグラフを作るとします。ここでまずxの数値を0.2刻みで作成していきます（さらに正確に計算したい場合は、0.2寄り数値を小さくするといい）。

その上で隣の列に=exp(xの数値記載列）と入力しましょう。

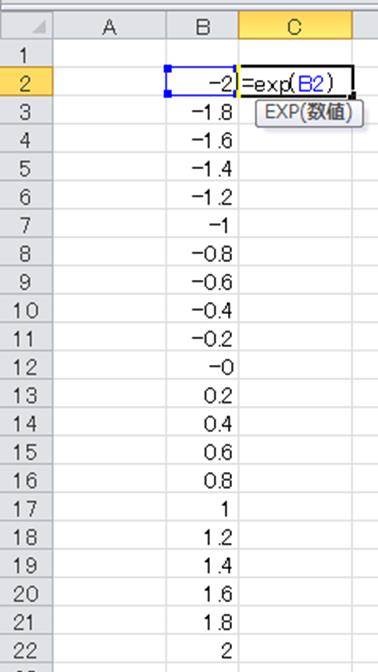
ENTERを押し、オートフィル機能（計算セルの右下に出る十字をダブルクリックなど）によって一括でexpの計算を実行させます。

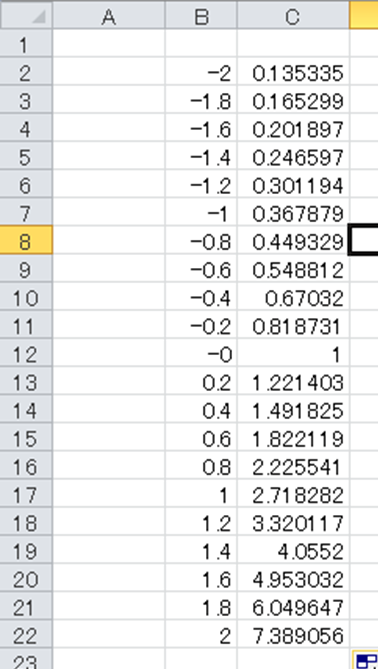
最後にこれら2行を選択の上、挿入、グラフ、散布図（曲線）と選択します。

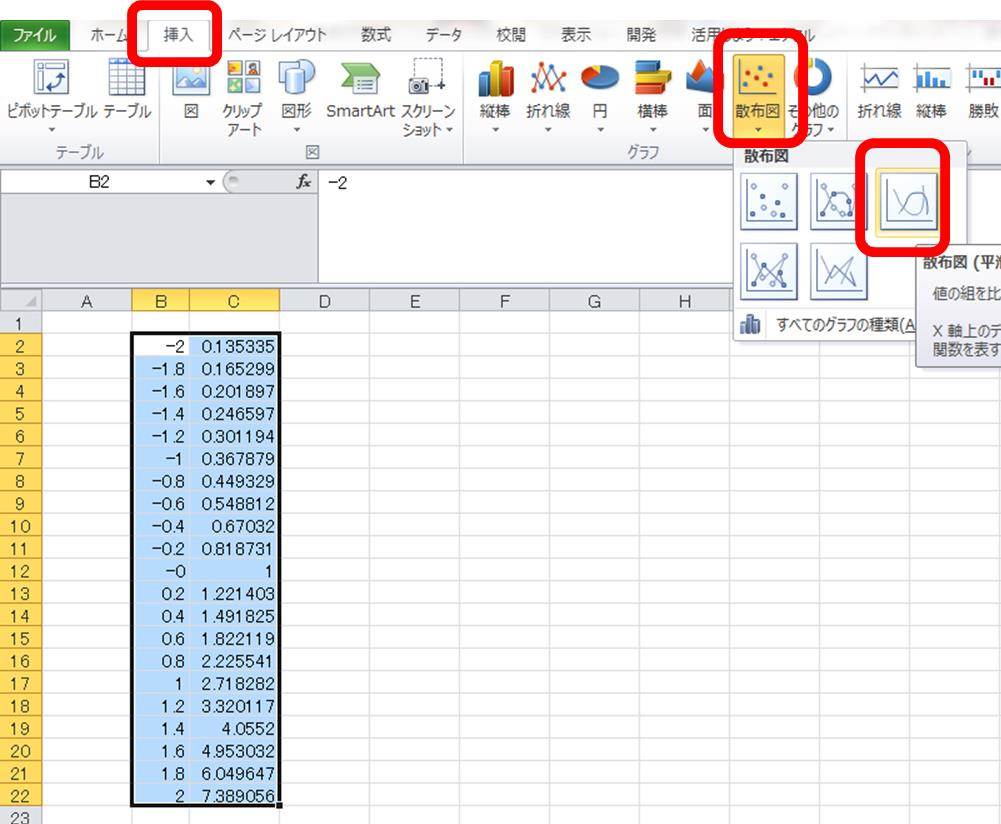
ENTERを押すと最初の指数関数expのグラフが完成となります。

なお指数関数的上昇や増加とはこのような指数関数のグラフが元となっていることも覚えておきましょう。

exp（x）の微分、つまりe^xの微分の公式も頻出ですので併せて理解しておくといいです。

具体的には、exp(x）を微分してもそのままexp(x）となります（言い換えるとe^xの微分はe^x）。

ここで（）内の数値が2xなどとなる場合、exp(2x）の微分は (2x)’ exp(2x）より2exp(2x）などと係数が前にかかることにも注意しましょう。

ここでは、指数関数のexpやeの意味や読み方、計算方法やグラフ、微分の公式について解説しました。

指数関数expの扱いは意外と難しいのでこの機会に覚えておくといいです。

さまざまな数式処理方法を理解し、毎日の生活に役立てていきましょう。