1から100までの偶数の和を計算する方法は？1から101までの奇数の和は？1から365までの和は？

算数や数学,SPIなどの問題として規則的な数列の足し算が必要となることがあります。

例えば、1から100まで足した数などの合計を求める問題が頻出ですが、簡単に解くにはどのように処理すればいいのか理解していますか。

ここでは、1から100までの和を簡単に計算する方法、1から50までの和、1から200までの和の計算方法と答えについて解説していきます。

1から100までの偶数の和の計算する方法

それでは、まず1から100までの偶数の数の合計を計算する方法について確認していきます。

偶数とはご存知のよう2,4,6など2で割り切れる数を意味しますが、これらの和の計算として「2+4+6+・・・」とやっていくとかなりの時間を要してしまいます。そのため簡単に解くための工夫を行うといいです。

具体的には、

・s=2+4＋6＋・・・＋98＋100とこれを逆に並べた

・s=100+98++・・・4+2

を縦に足していきましょう。

ここで1から100までの偶数の和をSとすると、2S＝（2+100）+（4+98）+・・・（98+4）+（100+2）＝102×100÷2と計算できるのがわかるでしょう。

よって、1から100までの偶数の和s＝102×100÷2÷2＝2550と求めることができるのです（※102が25個あると考えるといいです）。

これが1から100までの偶数の和を簡単に計算する方法です。

さらには1から101までの奇数を足しあわせてみましょう。基本的には上の1から100までの偶数の和の計算方法と同じでいいです。

具体的には、1から101までの奇数とは、1,3,5・・・99,101のことを指します。

1から101までの奇数の和をSとしますと、

２S＝（1+101）+（3+99）・・・（99+2）+（101+1）＝102×（（101ー1）÷2+1)＝102×51となります。50個でなく51個となることに注意しましょう。

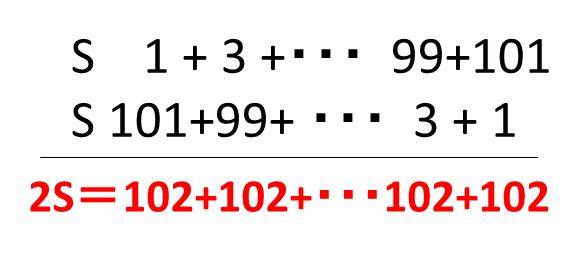
よってS＝102×51÷2＝2601と計算できました。

今度は100、101よりも大きな数値である365までの和の計算方法についても確認していきます。

考え方は上と同じでよく、最初と最後の数字を足したものに個数をかければいいわけです。

ここで1から365までの数の合計＝Sとすると、

２S＝（1+365）+（2+364）・・・（364+2）+（365+1）＝366×365となります。

よってS＝366×365÷2＝66795と計算できました。

各数値が変化しても基本的には同じように求めることができるので、是非この考え方を理解しておきましょう。

ここでは1から100までの偶数の和を計算する方法は？1から101までの奇数の和は？1から365までの和は？について確認しました。

等差数列の考え方を上手に活用し、更なる効率化を目指していきましょう、