数学の問題を解いたり、科学的な解析を行ったりする際に、よく三角関数の計算が必要となることが多いです。
中でも、三角関数を含んだ数式のグラフや微分の方法についての問題が出ることが多く、その解法について理解しておくといいです。
ここでは、この三角方程式の一つであるy=cos^2xのグラフやその周期、微分を行うとどうなるのかについて確認していきます。
y=cos^2xのグラフや周期はどうなるのか?【y=cos^2θ(2乗)のグラフ】
まず、y=cos^2xはy=cosxを2乗したものの数値であり、y=cos2xとは別物であることとを理解しておくといいです。またy=cos^2xとy=cos^2θは変数名が違うだけ意味は同じです。
代表的なx,yの数値を確認することで、y=cos^2xのグラフがどうなるのかについて確認します。
まずは、
・x=0の場合はcosx自体が1のため、y=cos^2xも1となります。
・x=30度の場合はcos30度が√3/2のため、y=cos^2x=3/4となります。
・x=45度の場合はcos30度が√2/2のため、y=cos^2x=1/2となります。
・x=60度の場合はcos30度が1/2のため、y=cos^2x=1/4となります。
・同様にx=90度の場合はcosx自体が0のため、y=cos^2x=0となります。
なお、90度を超えるとcosの数値がマイナスになりますが、cos^2xでは2乗をしているため、正の値となります。
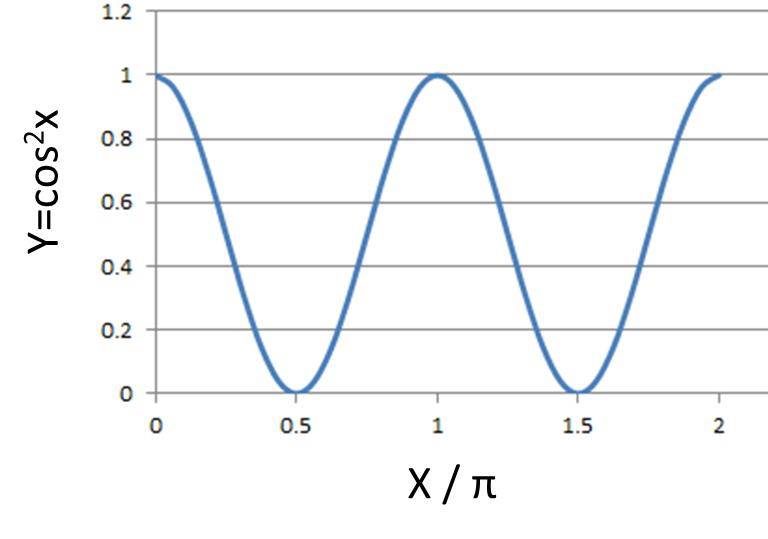
つまり、x=0~90度と90~180の範囲にて対称の軌跡がとられることになり、y=cos^2xのグラフは以下のような形状となります。
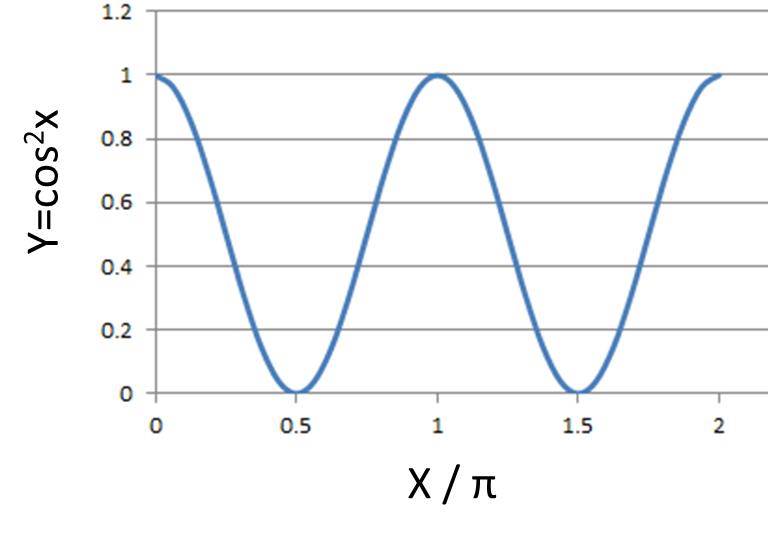
y=cos^2xのグラフのグラフは0~180度の軌跡が繰り返されることから、その周期はπであることがわかります。
y=cos^2xの綺麗なグラフを作成するためには、excelやpythonなどを活用していくといいです。
y=cos^2x( y=cos^2θ)を微分するとどうなるのか?
続いて、y= cos^2xの微分についても確認していきます。
まずは2乗の形であるため、その肩の係数が頭にきて、元の係数が1小さくなります。
よって、y’=( cos^2x)’= 2cosx(cosx)’=-2cosxsinx=-sin2xと計算することができるのです。途中でcosを微分した項を追加することを忘れないようにしましょう。
まとめ y=cos^2xのグラフや周期は?y=cos^2θを微分するとどうなるのか?
ここではy=cos^2xのグラフや周期は?y=cos^2θを微分するとどうなるのか?
・y=cos^2xとy=cos^2θは変数の表記が違うだけで同じもの
・y=cos^2xを微分した形はy=-sin2x=-2sinxcosx
・y=cos^2xとグラフは上の通りで周期はπ(180度)
となります。
y=cos^2x( y=cos^2θ)などのの方程式の扱いに慣れ、各種計算方法をマスターしていきましょう。
コメント