cosθ＝-1/2の角度（方程式）は？cosθ＝－√3/2（ルート3/2）やcosθ＝－√2/2（－1/√2）を満たす角度は何度？【単位円】

数学や物理などにおいて数値計算が必要となるケースは多いです。

中でも三角関数を含んだ計算を求められる割合が高いといえますが、その角度と数値の関係について理解していますか。

ここでは、特にcosθ（コサイン関数）の数値が-1/2、-1/√2（-√2/2）、－√3/2を満たすθの角度は何度なのかについて確認していきます。

cosθ＝-1/2の角度は何度【方程式と単位円におけるθの値】

それでは、単位円においてcosθ＝-1/2を満たす場合のθの角度が何度になるのかについて確認していきます。

結論からいますと、0≦θ≦2πの範囲においてcosθ＝-1/2を満たすθ＝120度、240度です。ラジアン表記の角度で考えるのであれば、θ＝2π/3、4π/3となります。

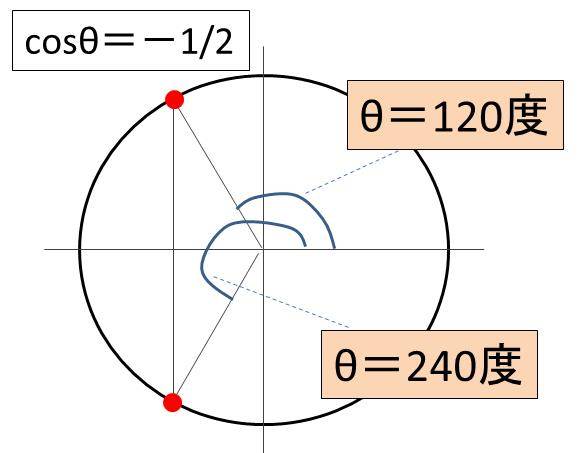
具体的には、cosθは単位円においてxの数値に着目すればよく、xが-1/2となるのは、120度と240度の2か所であることがわかります。

なお、θの範囲が狭く設定されているケースもあるので、注意してその角度を考えていきましょう。

続いて単位円においてcosθ＝-1/√2（-√2/2）を満たす場合のθの角度が何度になるのかについて確認していきます。

結論からいますと、0≦θ≦2πの範囲においてcosθ＝-1/√2を満たすθ＝135度、225度です。ラジアン表記の角度で考えるのであれば、θ＝3π/4、5π/4となります。

具体的には、cosθは単位円においてxの数値に着目すればよく、xが-1/√2（-√2/2）となる角度、135度と225度の2か所であることがわかります。

sinとcosを混同しないように注意していきましょう。

さらには、単位円においてcosθ＝-√3/2を満たす場合のθの角度が何度になるのかについて確認していきます。

結論からいますと、0≦θ≦2πの範囲においてcosθ＝-√3/2を満たすθ＝150度、210度です。ラジアン表記の角度で考えるのであれば、θ＝5π/6、7π/6となります。

上と同じようにcosθは単位円においてxの数値に着目すればよく、xが－ルート3/2となる角度、150度と210度の2か所であることがわかります。

ここでは、cosθ（コサイン関数）の数値が-1/2、-1/√2（-√2/2）、－ルート3/2を満たすθの角度は何度なのかについて解説しました。

・cosθ＝-1/2を満たすθの値＝120度、240度

・cosθ＝-1/√2（-√2/2）を満たすθの値＝135度、225度

・cosθ＝－√3/2を満たすθの値＝150度、210度

です。

三角関数の換算式になれ、毎日の生活に役立てていきましょう。