x=cosθ、y=cos2θの面積や曲線（グラフ）はどうなるのか？【媒介変数表記の図形】

イメージしにくい図形の代表として媒介変数表示の図形が挙げられます。

中でも差各関数が絡んでくると、いっそう容易にグラフを描きにくくなるため、その曲線を描く方法や面積を求める方法について理解しておくといいです。

ここでは、媒介変数で表す代表的な図形である、x=cosθ、y=cos2θやx=cosθ、y=sin2θのグラフ、面積の求め方について解説していきます。

x=cosθ、y=cos2θの図形の面積の計算方法

媒介変数表記の図形は、まずy=xの形に変換できないかを考えていくといいです。

ここで、y = cos2θ＝cos-2θ – sin-2θ ＝ 2cos^2θ－1 と式変形できます。なおx=cosθであることから上の図形は y=2x^2 -1 というyとxの数式に変換することができました。

そしてこのy=2x^2 -1は、二次曲線y=2×2 からy軸負の方向に1平行移動させたものといえ、以下のようなグラフとなります。

※

x=cosθ、y=cos2θの曲線（グラフ）のポイントとしては、

・y切片＝－1であること（ｘ＝０）
・x＝1でy＝1となること
・x＝2でy＝3となること
・y軸を元に左右対称であること

などです。

x=cosθ、y=cos2θで表される曲線（0≦θ≦π）とx軸で囲まれる図形の面積を求めていきましょう。

先にも述べたように、こちらの図形はy=2x^2 -1という数式で表されるため、これを単純に積分していけばいいのです。

なおθの範囲が0≦θ≦πを考慮しますと、－1≦x≦1という範囲を表しているともいえます。

結局は－1≦x≦1におけるはy=2x^2 -1の積分を行うとよく、

∫ydx＝∫ 2x^2 -1＝[2x^3 /3 + x ]＝（2/3 + 1）－（-2/3 +-1）＝10/3 と求めることができました。

なお、y軸に対して対称であることを考慮しますと、0≦x≦1の積分の2倍の値となることから、まずはそこを計算し2倍しても結果は同じとなります。

より計算する量を減らして、効率よく積分が実行できるようにさまざまな工夫を行っていきましょう。

ここでは、x=acosθとy=bsinθの面積の計算方法は？楕円の面積の一部の求め方は？【楕円の面積と円の面積】について解説しました。

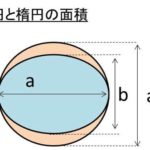
・x=acosθとy=bsinθは楕円で面積はπab

・一部の楕円の面積を求める際には、基本的に一部の円の面積を計算した倍率分の変換を行う

といいです。

楕円の面積を始めとして、各種図形の計算方法をマスターしていきましょう。