x=acosθとy=bsinθの面積の計算方法は？楕円の面積の一部の求め方は？【楕円の面積と円の面積】

科学的な解析を行う際に様々な図形の面積が必要となることがあり、この面積が求められないと処理自体ができなくなってしまいます。

そのため面積計算は重要なわけですが、楕円を表すx=acosθとy=bsinθで表される図形の面積を求める方法について理解していますか。

ここでは、、x=acosθとy=bsinθの面積の計算方法や楕円と円の面積の違いや計算方法について解説していきます。

x=acosθとy=bsinθの面積の計算方法は【楕円の面積と円の面積】

まず円の面積の公式は円周率をπ、半径をaとした場合はπa＾2（基本的には半径rとし、πr^2ですが、楕円との比較のためのこう記載）と表現されます。

一方で楕円とは、この円の縦もしくは横に拡大・拡大縮小させた図形であるため、「楕円の面積は元の円の面積を拡大・縮小分の割合をかけたもの」に相当します。

例えは長径がa、短径がb（a×b/a倍したもの）の楕円であればπabと記載することができるのです。

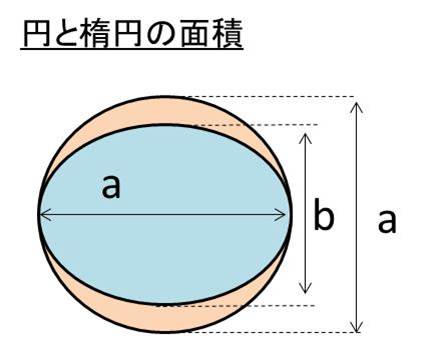
なお、x=acosθ、y=bsinθはまx方向の径がa、y方向の長さがbとなったものであり、まさに上の楕円そのものとなります。よってこの楕円の面積は、πabと表されます。

それでは、媒介変数θで表される上式が楕円となることも確認していきます。

cosθ^2 + sinθ^2 =1 という関係式と、cosθ＝x/a、sinθ=y/bをかつ移用していくと、x^2/a^2 + y^2/b^2 =1 という楕円の公式そのものに変形することができます。

これで、x=acosθ、y=bsinθが楕円となることが証明されました。

なお、上のような媒介変数表記の楕円のみでなく、計算がややこしいものに一部の楕円の面積が挙げられます。扇形をつぶしたような形状の楕円の面積などです。

具体的には、以下のよう中心角が45度でx方向の長さが2、y方向の長さが1の楕円の面積を考えてみましょう。

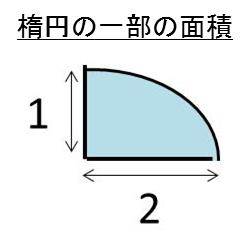
このとき楕円の元となる円の一部（つまり扇形）の面積を考えて、楕円の面積に帰る際の変換倍率をかけていけばいいのです。

具体的には、元の円（半径2cm）をベースとした中心角45どの扇形の面積はπ2^2 ×45/360＝π/2と計算できます。

この扇形の面積を1/2倍すると、上の楕円の一部の面積となるので、π/2 ÷ 2 = π/4 と求めることができるのです。

ここでは、x=acosθとy=bsinθの面積の計算方法は？楕円の面積の一部の求め方は？【楕円の面積と円の面積】について解説しました。

・x=acosθとy=bsinθは楕円で面積はπab

・一部の楕円の面積を求める際には、基本的に一部の円の面積を計算した倍率分の変換を行う

といいです。

楕円の面積を始めとして、各種図形の計算方法をマスターしていきましょう。