lnxを微分すると何？lnaxやlnx^2(logx^2)の微分は？微分してlogxになるf(x)は？

科学的な解析を行う際に、よく数値計算が必要となることがあります。

中でも対数関数のln（logeとも記載）の微分などが苦手と感じる人が多いですが、あなたがはこの自然対数のln(x)（loge(x)）の各計算方法について理解していますか

ここでは、自然対数のlnxを微分すると何？lnaxやlnx^2(logx^2)の微分は？微分してlogxになるf(x)は？について詳しく解説していきます。

ln(x)を微分すると何？【logex】

結論からいいますと、自然対数のln(x)と微分すると1/xとなります。

なお、元の式log e x（底がeと書く）やlog x（eは略す）などとも記載する場合があるので注意が必要です。

これは対数関数の微分計算を行う上の基礎となるので、理解しておくといいです。

そのため、

・2lnxを微分すると 2/x

・3lnxを微分すると 3/x

などともなることを覚えておきましょう。

今度はlnの（）内に数字と記号が入っている（一般式でlnaxと書けるもの）場合の微分方法についても確認していきます。

ln(ax)と表記できる関数を微分すると、 (ax)’/ax ＝ a/ax = 1/x と上のlnxを微分した形と同じとなるのです。

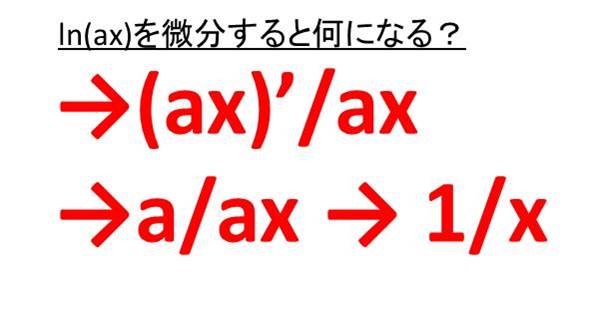
この時、aの数値が何でもこのようになります。面白いですね

例えば、

・ln(2x)の微分は 2/2xより 1/x

などといった具合です。

今度はlnx全体の2乗（logxの2乗）の微分についても確認していきます。

まずはある関数の2乗の微分のため、この型の数値が前にでてきて、その次数が1減ります。さらに、2乗の中身だった関数を微分したものも掛け合わせる必要があるため、

2lnx （lnx）’ より、 (lnx)^2の微分は　2lnx/xと求めることができました。

なお、lnxではなくlogxなども記載するから、(logx)^2の微分は　2logx/xとあるとも覚えておきましょう。

最後に微分しg手logxになる関数についても確認していきます。微分してlogxとなる関数（fx）を求めたいということは、単純に積分をするといいです。

具体的には、∫ logx dx について部分積分を行っていくと、

∫ logx dx = 【xlogx】－ ∫x (logx)’ dx ⇔ xlogx ー x/x +C ⇔ slogx － 1 + C が答えであることがわかりました。

ここでは、微分してlogxになるf(x)は？lnx(logex)を微分すると何？lnaxやlnx^2(logx^2)の微分は？について解説しました。

lnxに関する微分や積分は頻出ですので、この機会にぜひ覚えておくといいです。

lnをはじめとした数値計算に慣れ、日々の解析に役立てていきましょう。