私たちが何気なく生活している中で時間・時計に関する疑問がわいてくることがあるでしょう。
例えば、時計において長い針や短い針に着目した場合、各々が重なる(追い越す)時刻がいつなのかを計算するにはどのように処理すればいいのか理解していますか。
ここでは、この時計において長針と短針が重なる時刻や回数の求め方として、1時から2時の間、3時から4時の間、6時から7時の間という具体的な例を挙げて解説していきます。
1時から2時の間で長針と短針が重なる時刻や回数は?【時計】
それでは、まず1時から2時の間で長針と短針が重なる時刻や回数は?について確認していきます。
時計において長針と短針が重なる時刻の計算は
・開始時刻(今回は1時)における長針と短針の角度
・長針の移動速度(角度)
・短針の移動速度(角度)
が解くためのカギとなります。
まず1時の場合では、長針と短針のなす角度は30度(360 ÷12=30より)であり、短針の方が長針よりも先に位置しているような関係となります。
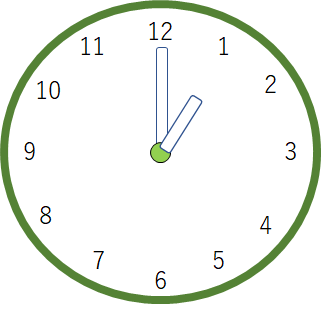
なお、長針は1時間=60分で1週(360度)回転することから、1分あたりでは360÷60 =6度移動していることになります。
同様に短針では12時間=720分で1週(360度)回転することから、1分あたりでは360÷720 =0.5度移動していることになります。
よって1分当たりで長針は短針よりも5.5度分、進んでいることになるわけです。
よって、1時から2時において時計の長針と短針が重なる時刻としては、30 ÷ 5.5 = 30 ÷ 55/10 = 30 ×10 /55 = 5と25/55 = 5と5/11分後となるのです。
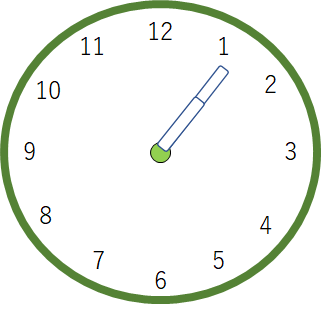
答えは1時5と5/11分後に長針と短針が重なるのがわかりました。
計算が複雑になるのでミスには注意しましょう。
3時から4時の間で長針と短針が重なる時刻や回数は?【時計】
続いて3時から4時の間で長針と短針が重なる時刻や回数は?について確認していきます。
上と同様に時計において長針と短針が重なる時刻の計算は、
・開始時刻(今回は3時)における長針と短針の角度
・長針の移動速度(角度)
・短針の移動速度(角度)
が解くためのカギとなります。
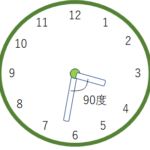
上述の問題と異なるのは「開始時の長針と短針の角度のみ」であり、3時の場合では90度となります。
さらに、長針は短針よりも1分あたり5.5度大きく動くことを考慮しますと、
3時から4時において時計の長針と短針が重なる時刻としては、90 ÷ 5.5 = 90 ÷ 55/10 = 90 ×10 /55 =16と20/55 = 16と4/11分後となるのです。
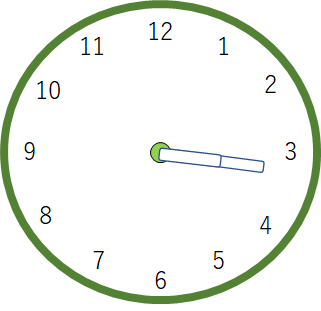
答えは3時16と4/11分後に長針と短針が重なるのがわかりました。
6時から7時の間で長針と短針が重なる時刻や回数は?【時計】
さらには、6時から7時の間で長針と短針が重なる時刻や回数は?について確認していきます。
上と同様に時計において長針と短針が重なる時刻の計算は
・開始時刻(今回は6時)における長針と短針の角度
・長針の移動速度(角度)
・短針の移動速度(角度)
が解くためのカギとなります。
上述の問題とことなるのは、開始時の長針と短針の角度のみであり、6時の時は180度となります
さらに、長針は短針よりも1分あたり5.5度大きく動くことを考慮しますと、
6時から7時において時計の長針と短針が重なる時刻としては、180 ÷ 5.5 = 180 ÷ 55/10 = 180 ×10 /55 =32と40/55 = 32と8/11分後となるのです。
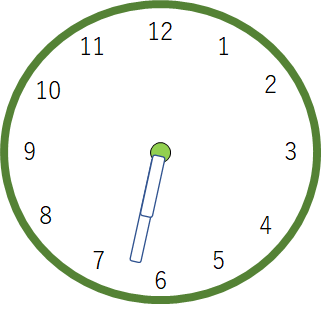
答えは6時32と8/11分後に長針と短針が重なるのがわかりました。
なお長針と短針が重なる回数は各々の時間帯にて1回のみ(1時間に1回)といえますね。
まとめ 6時から7時で時計の長針と短針が重なる時刻や回数は?
ここでは、時計において長針と短針が重なる時刻や回数は?1時から2時、3時と4時の間、6時と6時の間での時刻は?について確認しました。
時計の性質は生活していく上でも大切なので、この機会に覚えておくといいです。
時計の性質を始めとして日常の知識を身につけることによって、日々の生活を楽しんでいきましょう。


コメント