243を素因数分解すると？247を素因数分解すると？素数か

コンピュータ処理や数学・算数などの勉強を行う際に「素因数分解や素数かどうかの判定」が求められることがあります。

ただ、これら素因数分解や素数かどうかの判定は苦手な人が多いです。

ここでは、数値の「243と247」に着目して、243の素因数分解は？247の素因数分解は？素数か？について実際の計算過程も踏まえて確認していきます。

243を素因数分解するとどうなる？素数か？

それでは以下で243を素因数分解していきます。

結論からいいますと243を素因数分解すると3×3×3×3×3（5回かける）となります。

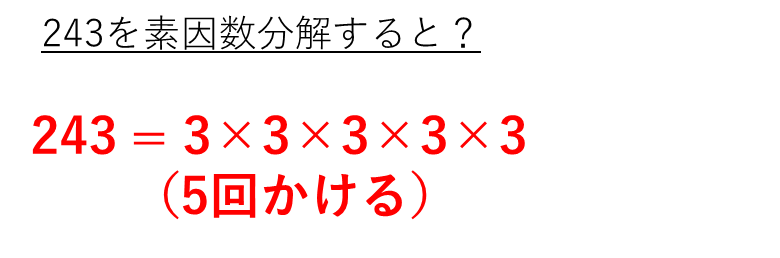
256を素因数分解するには、小さい数で順々に割っていくといいです（例えば、÷2をする、÷3をする・・など）。

具体的には

・243 ＝ 3×81
→243 = 3×3×27
→243 = 3×3×3×9
→243 = 3×3×3×3×3

となるわけです。

このように243には1と243以外にも約数があるため、素数ではありません。

続いて、247を素因数分解していきます。

結論からいいますと247を素因数分解すると13×19となります。247は素数ではありません。

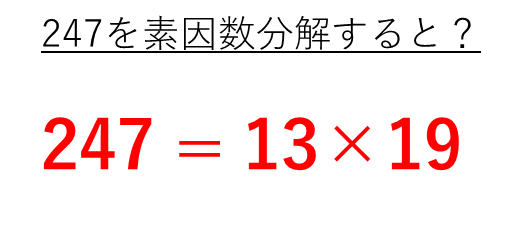
247を素因数分解するには、小さい数で順々に割っていくといいです（例えば、÷2をする、÷3をする・・など）。

ただ247はなかなか割れるものが見つからず、一見すると素数？と勘違いしやすいです。

具体的には11で割ることができ

・247 ＝ 13×19

となるわけです。

このように、247には1と247以外にも約数があるため、素数ではありません。

ここでは、243を素因数分解すると？247を素因数分解すると？素数か？について解説しました。

243や247だけでなく、どのような数値であっても素因数分解や素数かどうかの判定は難しい傾向にあるため、この機会に理解しておくといいです。

さまざまな計算処理に慣れ、日々の生活に役立てていきましょう。