物理においてよく出題される問題は決まっており、そのパターンや公式をまず覚えておくといいです、
例えば、鉛直投げ上げにてv=v0-gtの公式が頻出ですが、この鉛直投げ上げの公式がなぜ成立するのか理解していますか。
ここでは、鉛直投げ上げの速度の公式(v=v0-gt)はなぜ成り立つのか?鉛直投げ上げ時の地面ん位落下するまでの時間、鉛直投げ上げ時の地面に達する直前の速さ、変位などについて解説していきます。
鉛直投げ上げと速度や変位の公式は?【v=v0-gtはなぜ】
まずは鉛直投げ上げ時の速度について考えていきます。
上方向を正とし、初期速度をv0と置きます。このとき、重力加速度gは負の方向にかかるため、時間をtとした場合のtにおける速度v=v0-gtと計算することができるのです。
徐々に初期速度より低下し、最高点まで到達したら速度がマイナスとなり、向きが変わると理解しておくといいです。
なお、鉛直投げ合挙げ時の変異の公式としてはh=v0t – 1/2 gt^2といえます。
さらには、v02 – v2=2ghよう公式もあり、こちらは時間の項を含まないため、位置さえわかれば計算できる便利な式のため、覚えておきましょう。
鉛直投げ上げ時の最高点までの時間と変位は?
なお、鉛直投げ上げにおける最高点までに到達するまでにかかる時間を考えるときには、速度に着目します。
具体的には、速度が0となる際に、最高点に到達しているため、
V=v0-gt=0という式を立てるといいわけです。
よって、これを解くと鉛直投げ上げ時の最高点までの時間t=V0/gと求めることができるのです。
さらに、最高点における変位はこのtを公式に代入していけばいいので、
h=v0t – 1/2 gt^2=V0 (V0/g)- 1/2 g(V0/g)^2=1/2 V0^2/gと求めることができました。
なお、V02―v2=2ghの式を活用すると、鉛直投げ上げ時に最高点に到達する場合には V0^2=2gh⇔ h= v0^2 / 2g とより簡単に計算できることも覚えておきましょう。
鉛直投げ上げ時の地面に落下するまでの時間、鉛直投げ上げ時の地面に達する直前の速さの計算方法は?【鉛直投げ上げでは最高点にいく時間と元の位置に戻る時間は同じ】
同様に、鉛直投げ上げ時における地面に到達するまでの時間も考えていきましょう。
鉛直投げ上げにおいて、投げた球が地面に落下するということは、元の位置と同じ位置、つまり変位が0であることを意味します。
つまり、h=v0t – 1/2 gt^2の公式において、h=0とすればいいので、 V0= 1/2 gtより t=2V0/gと計算できます。
なお、鉛直投げ上げにおける最高点までの時間がt=V0/gであることから、地面に落下するまでの時間の半分であることがわかります、結局のところ、最高点に達するまでの時間とそこから地面に到達するまでの時間は同じことがわかるのです。
なお、鉛直投げ上げにおける地面に到達する際の直前の時間は、v02 – v2=2ghにおいてh=0とおけばいいので、V=V0と初速度と同じで向きが逆であることを理解しておきましょう。
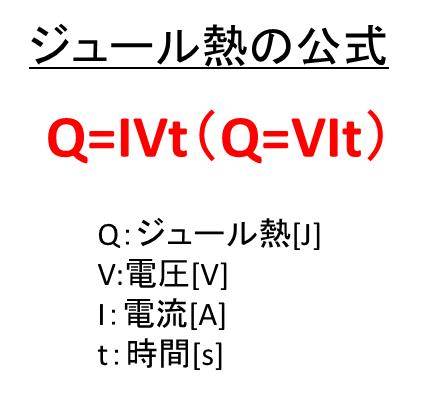
まとめ Q=ivt(Q=vit)やQ=I2Rtといったジュール熱の公式と計算方法と単位や記号と抵抗との関係【ジュール熱は抵抗と比例するのか?
ここでは、ジュール熱の記号や単位、電流、電圧、抵抗、電力との関係などについて確認しました。
・Q=ivt(Q=vit)
・Q=I2Rt
と求められることを理解しておくといいです。
電気的な用語やその公式、それを活用した計算方法を理解し毎日の業務に活用していきましょう。

コメント