数学や物理の問題解く際によく数値計算が必要となることがあります。
中でも対数に関する計算も頻出ですが、その解き方は難しいことが多く、きちんと理解しておくことが大切です。
ここでは、この対数の計算問題として「log10 2からlog10 5を求める方法」「log10 2=a log10 3=b とする時のlog10 15の計算方法」「log2 10 の近似値の覚え方」について解説していきます。
log10 2の近似値の覚え方や求め方【0.3010】
それではまずlog10 2の近似値やその覚え方、求め方について解説していきます。
結論からいいますと、log10 2 の近似値=0.3010となります。
覚え方としては語呂合わせとして「0.3010 → おさまるてん、おっさん多い」などと暗記したり、31という数値のみを暗記し、間に0が入るなどと理解しておくのがおすすめですね。
特に語呂合わせの場合は、上のようなものだけでなくあなた自身がしっくりくるものを挙げ、それを覚えるようにすると忘れにくいです。
なお、log10 2の求め方として厳密なものは高校数学では習わず、基本的にはエクセルや関数電卓で計算するしかないです。
エクセルでこのlog10 2を計算したい場合は、以下のようセル内で=log10(2)と入力し、ENTERをおすだけでいいです。
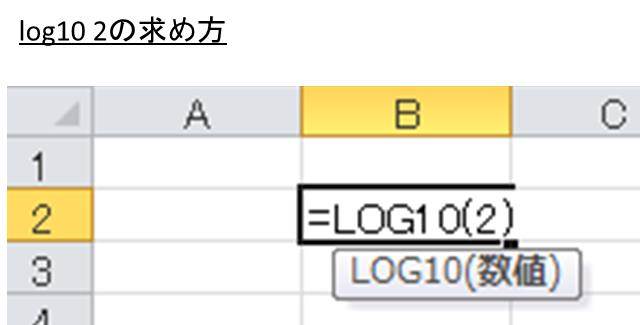
なお、基本的にはlog10 2の近似値の0.3010と覚えておけばいいでしょう。
log10 2からlog10 5を求める方法は?
続いて頻出問題のlog10 2が既知の時に、log10 5を計算する方法を確認していきます。
ここで、10 ÷ 2 =10/2 = 5という関係式を活用していきます。
するとlog10 5= log10(10/2) = log10 10 - log10 2 =1 - 0.3010 =0.699 と求めることができるのです。

ポイントとしては上手くlog10 2の数値を使える形にするよう式変形することといえます。
log10 2=a log10 3=b とする時のlog10 15の計算方法【log10 2=p log10 3=q】
さらには、log10 2=a log10 3=b(log10 2=p log10 3=qなどの場合もあり) とする時のlog10 15の求め方について確認していきます。
こちらもlog10 15を上手く式変形させ、log10 2=a log10 3=b が出てくるものを考えるのがポイントです。
具体的に15 = 3 × 5 = 3 × 10/2 となることから、
log10 15 = log10 (3 × 10/2) = log10 3 + log10 10 - log10 2 =1 - a + bと変換できることがわかりました。
まとめ log10 2=a log10 3=b(log10 2=p log10 3=q)とする時の計算方法など
ここでは、対数に関する「log10 2からlog10 5を求める方法」「log10 2=a log10 3=b とする時のlog10 15の計算方法」「log2 10 の近似値の覚え方」について解説しました。
対数での計算はややこしいことが多いので、出来る限りたくさんの問題を解いて慣れていくといいです。
対数を始めとした数値計算に慣れ、毎日の生活に役立てていきましょう。


コメント