3と6の最小公倍数は？3と8の最小公倍数は？3と9の最小公倍数は？

算数・数学の計算やSPIの問題を解く際に最小公倍数を求める必要が出てくることがあります。

中でも最小公倍数の問題としてわかりにくいものに3と6の最小公倍数、3と8の最小公倍数、3と9の最小公倍数などがありますが、これらの解き方について理解していますか。

ここでは、この最小公倍数の求め方の具体例として3と6の最小公倍数は？3と8の最小公倍数は？3と9の最小公倍数は？について解説していきますので、参考にしてみてください。

3と6の最小公倍数は？

それでは以下で3と6の最小公倍数の計算方法について確認していきます。

まず最小公倍数とは、各々の数を2倍、3倍・・・としていった際に、最初に出てくる同じ数値を指します。

具体例として3と6の最小公倍数を求めていきましょう。

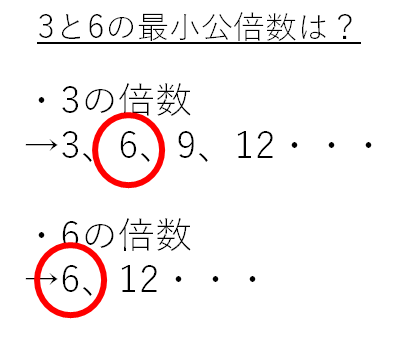
まずは3と6の各々の倍数を上げます。

・3の倍数

→3、6、9、12・・・

・6の倍数

→6、12・・・

となるわけです。

この時「6」が3と6の両方の倍数として最初に表れているために、これが3と6の最小公倍数にあたることがわかりました（公倍数の中で最も小さいから最小公倍数）

なお、そもそも6は3の約数（3で割り切れる）であることから「すぐに6そのものが最小公倍数と判断できる」と覚えておくといいですね。

なお基本的に最小公倍数の数え上げでは、大きい方の数字の倍数を先にあげ（今回では6の倍数）、その中に「もう一方の数字の倍数がないか」と確認する方が効率よく求められるためぜひ試してみてくださいね。

続いて、3と8との最小公倍数についても見ていきましょう。

上と同じように各々の倍数を出します。

・3の倍数

→3、6、9、12、15、18、21、24・・・

・8の倍数

→8、16、24・・・

すると、24の最初の3と8の公倍数のため、これが3と8の最小公倍数となることがわかりました。

3と8のように各々の約数（割り切れる数）が共通していない場合では、各々を掛け合わせたものが最小公倍数となることも理解しておきましょう。

さらに、3と9との最小公倍数についても見ていきましょう。

上と同じように各々倍数を出します。

・3の倍数

→3、6、9・・・

・9の倍数

→9・・・

すると「9」の最初の3と9の公倍数のため、これが3と9の最小公倍数となることがわかりました。

上の3と6の最小公倍数と同様に、9は3の約数であるため「９そのものが最小公倍数となる」パターンですね。

ここでは、3と6の最小公倍数は？3と8の最小公倍数は？3と9の最小公倍数は？という問題を通して、最小公倍数の求め方を解説しました。

慣れていないと最小公倍数の計算は対応できないため、この機会に覚えておくといいです。

さまざまな計算を学び、日々の生活に役立てていきましょう。